In the social science problems I've seen, Ockham's razor is at best an irrelevance

TO BE NOTED: From Statistical Modeling, Causal Inference, and Social Science:

( Albert Einstein
"Everything should be made as simple as possible, but not simpler." NB DON )


"Bayes, Jeffreys, prior distributions, and the philosophy of statistics

By Andrew Gelman on May 7, 2009 8:32 PM | 2 Comments

Christian Robert, Nicolas Chopin, and Judith Rousseau wrote this article that will appear in Statistical Science with various discussions, including mine.

I hope those of you who are interested in the foundations of statistics will read this. Sometimes I feel like banging my head against a wall, in my frustration in trying to communicate with Bayesians who insist on framing problems in terms of the probability that theta=0 or other point hypotheses. I really feel that these people are trapped in a bad paradigm and, if they would just think things through based on first principles, they could make some progress. Anyway, here's what I wrote:

I actually own a copy of Harold Jeffreys's Theory of Probability but have only read small bits of it, most recently over a decade ago to confirm that, indeed, Jeffreys was not too proud to use a classical chi-squared p-value when he wanted to check the misfit of a model to data (Gelman, Meng, and Stern, 2006). I do, however, feel that it is important to understand where our probability models come from, and I welcome the opportunity to use the present article by Robert, Chopin, and Rousseau as a platform for further discussion of foundational issues.

In this brief discussion I will argue the following: (1) in thinking about prior distributions, we should go beyond Jeffreys's principles and move toward weakly informative priors; (2) it is natural for those of us who work in social and computational sciences to favor complex models, contra Jeffreys's preference for simplicity; and (3) a key generalization of Jeffreys's ideas is to explicitly include model checking in the process of data analysis

The role of the prior distribution in Bayesian data analysis

At least in the field of statistics, Jeffreys is best known for his eponymous prior distribution and, more generally, for the principle of constructing noninformative, or minimally informative, or objective, or reference prior distributions from the likelihood (see, for example, Kass and Wasserman, 1996). But it can notoriously difficult to choose among noninformative priors; and, even more importantly, seemingly noninformative distributions can sometimes have strong and undesirable implications, as I have found in my own experience (Gelman, 1996, 2006). As a result I have become a convert to the cause of weakly informative priors, which attempt to let the data speak while being strong enough to exclude various "unphysical" possibilities which, if not blocked, can take over a posterior distribution in settings with sparse data--a situation which is increasingly present as we continue to develop the techniques of working with complex hierarchical and nonparametric models.

How the social and computational sciences differ from physics

Robert, Chopin, and Rousseau trace the application of Ockham's razor (the preference for simpler models) from Jeffreys's discussion of the law of gravity through later work of a mathematical statistician (Jim Berger), an astronomer (Bill Jefferys), and a physicist (David MacKay). From their perspective, Ockham's razor seems unquestionably reasonable, with the only point of debate being the extent to which Bayesian inference automatically encompasses it.

My own perspective as a social scientist is completely different. I've just about never heard someone in social science object to the inclusion of a variable or an interaction in a model; rather, the most serious criticisms of a model involve worries that certain potentially important factors have not been included. In the social science problems I've seen, Ockham's razor is at best an irrelevance and at worse can lead to acceptance of models that are missing key features that the data could actually provide information on. As such, I am no fan of methods such as BIC that attempt to justify the use of simple models that do not fit observed data. Don't get me wrong--all the time I use simple models that don't fit the data--but no amount of BIC will make me feel good about it! (See Gelman and Rubin (1995) for a fuller expression of this position, and Raftery (1995) for a defense of BIC in general and in the context of two applications in sociology.)

I much prefer Radford Neal's line from his Ph.D. thesis:

Sometimes a simple model will outperform a more complex model . . . Nevertheless, I [Neal] believe that deliberately limiting the complexity of the model is not fruitful when the problem is evidently complex. Instead, if a simple model is found that outperforms some particular complex model, the appropriate response is to define a different complex model that captures whatever aspect of the problem led to the simple model performing well.

This is not really a Bayesian or a non-Bayesian issue: complicated models with virtually unlimited nonlinearity and interactions are being developed using Bayesian principles. See, for example, Dunson (2006) and Chipman, George, and McCulloch (2008). To put it another way, you can be a practicing Bayesian and prefer simpler models, or be a practicing Bayesian and prefer complicated models. Or you can follow similar inclinations toward simplicity or complexity from various non-Bayesian perspectives.

My point here is only that the Ockhamite tendencies of Jeffreys and his followers up to and including MacKay may derive to some extent from the simplicity of the best models of physics, the sense that good science moves from the particular to the general--an attitude that does not fit in so well with modern social and computational science.

Bayesian inference vs. Bayesian data analysis

One of my own epiphanies--actually stimulated by the writings of E. T. Jaynes, yet another Bayesian physicist--and incorporated into the title of my own book on Bayesian statistics, is that sometimes the most important thing to come out of an inference is the rejection of the model on which it is based. Data analysis includes model building and criticism, not merely inference. Only through careful model building is such definitive rejection possible. This idea--the comparison of predictive inferences to data--was forcefully put into Bayesian terms nearly thirty years ago by Box (1980) and Rubin (1984) but is even now still only gradually becoming standard in Bayesian practice.

A famous empiricist once said, "With great power comes great responsibility." In Bayesian terms, the stronger we make our model--following the excellent precepts of Jeffreys and Jaynes--the more able we will be to find the model's flaws and thus perform scientific learning.

To roughly translate into philosophy-of-science jargon: Bayesian inference within a model is "normal science," and "scientific revolution" is the process of checking a model, seeing its mismatches with reality, and coming up with a replacement. The revolution is the glamour boy in this scenario, but, as Kuhn (1962) emphasized, it is only the careful work of normal science that makes the revolution possible: the better we can work out the implications of a theory, the more effectively we can find its flaws and thus learn about nature. In this chicken-and-egg process, both normal science (Bayesian inference) and revolution (Bayesian model revision) are useful, and they feed upon each other. It is in this sense that graphical methods and exploratory data analysis can be viewed as explicitly Bayesian, as tools for comparing posterior predictions to data (Gelman, 2003).

To get back to the Robert, Chopin, and Rousseau article: I am suggesting that their identification (and Jeffreys's) of Bayesian data analysis with Bayesian inference is limiting and, in practice, puts an unrealistic burden on any model.

Conclusion

If you wanted to do foundational research in statistics in the mid-twentieth century, you had to be bit of a mathematician, whether you wanted to or not. As Robert, Chopin, and Rousseau's own work reveals, if you want to do statistical research at the turn of the twenty-first century, you have to be a computer programmer.

The present discussion is fascinating in the way it reveals how many of our currently unresolved issues in Bayesian statistics were considered with sophistication by Jeffreys. It is certainly no criticism of his pioneering work that it has been a springboard for decades of development, most notably (in my opinion) involving the routine use of hierarchical models of potentially unlimited complexity, and with the recognition that much can be learned by both the successes and the failures of a statistical model's attempt to capture reality. The Bayesian ideas of Jeffreys, de Finetti, Lindley, and others have been central to the shift in focus away from simply modeling data collection and toward the modeling of underlying processes of interest--"prior distributions," one might say.

[References (and a few additional footnotes) appear in the posted article.]"

To many minds this unexplained coincidence is a blemish on the face of an otherwise rather attractive structure

TO BE NOTED: From In The Dark:

"The Cosmic Tightrope

Here’s a thought experiment for you.

Imagine you are standing outside a sealed room. The contents of the room are hidden from you, except for a small window covered by a curtain. You are told that you can open the curtain once and only briefly to take a peep at what is inside, and you may do this whenever you feel the urge.

You are told what is in the room. It is bare except for a tightrope suspended across it about two metres in the air. Inside the room is a man who at some time in the past - you’re not told when - began walking along the tightrope. His instructions were to carry on walking backwards and forwards along the tightrope until he falls off, either through fatigue or lack of balance. Once he falls he must lie motionless on the floor.

You are not told whether he is skilled in tightrope-walking or not, so you have no way of telling whether he can stay on the rope for a long time or a short time. Neither are you told when he started his stint as a stuntman.

What do you expect to see when you eventually pull the curtain?

Well, if the man does fall off sometime it will clearly take him a very short time to drop to the floor. Once there he has to stay there.One outcome therefore appears very unlikely: that at the instant you open the curtain, you see him in mid-air between a rope and a hard place.

Whether you expect him to be on the rope or on the floor depends on information you do not have. If he is a trained circus artist, like the great Charles Blondin here, he might well be capable of walking to and fro along the tightrope for days. If not, he would probably only manage a few steps before crashing to the ground. Either way it remains unlikely that you catch a glimpse of him in mid-air during his downward transit. Unless, of course, someone is playing a trick on you and someone has told the guy to jump when he sees the curtain move.

This probably seems to have very little to do with physical cosmology, but now forget about tightropes and think about the behaviour of the mathematical models that describe the Big Bang. To keep things simple, I’m going to ignore the cosmological constant and just consider how things depend on one parameter, the density parameter Ω₀. This is basically the ratio between the present density of the matter in the Universe compared to what it would have to be to cause the expansion of the Universe eventually to halt. To put it a slightly different way, it measures the total energy of the Universe. If Ω₀>1 then the total energy of the Universe is negative: its (negative) gravitational potential energy dominates over the (positive) kinetic energy. If Ω₀<1>0=1 exactly then the Universe has zero total energy: energy is precisely balanced, like the man on the tightrope.

A key point, however, is that the trade-off between positive and negative energy contributions changes with time. The result of this is that Ω is not fixed at the same value forever, but changes with cosmic epoch; we use Ω₀ to denote the value that it takes now, at cosmic time t₀, but it changes with time.

At the beginning, at the Big Bang itself, all the Friedmann models begin with Ω arbitrarily close to unity at arbitrarily early times, i.e. the limit as t tends to zero is Ω=1.

In the case in which the Universe emerges from the Big bang with a value of Ω just a tiny bit greater than one then it expands to a maximum at which point the expansion stops. During this process Ω grows without bound. Gravitational energy wins out over its kinetic opponent.

If, on the other hand, Ω sets out slightly less than unity – and I mean slightly, one part in 10⁶⁰ will do – the Universe evolves to a state where it is very close to zero. In this case kinetic energy is the winner and Ω ends up on the ground, mathematically speaking.

In the compromise situation with total energy zero, this exact balance always applies. The universe is always described by Ω=1. It walks the cosmic tightrope. But any small deviation early on results in runaway expansion or catastrophic recollapse. To get anywhere close to Ω=1 now - I mean even within a factor ten either way - the Universe has to be finely tuned.

A slightly different way of describing this is to think instead about the radius of curvature of the Universe. In general relativity the curvature of space is determined by the energy (and momentum) density. If the Universe has zero total energy it is flat, so it doesn’t have any curvature at all so its curvature radius is infinite. If it has positive total energy the curvature radius is finite and positive, in much the same way that a sphere has positive curvature. In the opposite case it has negative curvature, like a saddle. I’ve blogged about this before.

I hope you can now see how this relates to the curious case of the tightrope walker.

If the case Ω₀= 1 applied to our Universe then we can conclude that something trained it to have a fine sense of equilibrium. Without knowing anything about what happened at the initial singularity we might therefore be pre-disposed to assign some degree of probability that this is the case, just as we might be prepared to imagine that our room contained a skilled practitioner of the art of one-dimensional high-level perambulation.

On the other hand, we might equally suspect that the Universe started off slightly over-dense or slightly under-dense, at which point it should either have re-collapsed by now or have expanded so quickly as to be virtually empty.

About fifteen years ago, Guillaume Evrard and I tried to put this argument on firmer mathematical grounds by assigning a sensible prior probability to Ω based on nothing other than the assumption that our Universe is described by a Friedmann model.

The result we got was that it should be proportional to (Ω|Ω-1|)^-1. I was very pleased with this result, which is based on a principle advanced by Ed Jaynes, but I have no space to go through the mathematics here. Note, however, that this prior has three interesting properties: it is infinite at Ω=0 and Ω=1, and it has a very long “tail” for very large values of Ω. It’s not a very well-behaved measure, in the sense that it can’t be integrated over, but that’s not an unusual state of affairs in this game. In fact it is an improper prior.

I think of this prior as being the probabilistic equivalent of Mark Twain’s description of a horse:

dangerous at both ends, and uncomfortable in the middle.

Of course the prior probability doesn’t tell usall that much. To make further progress we have to make measurements, form a likelihood and then, like good Bayesians, work out the posterior probability . In fields where there is a lot of reliable data the prior becomes irrelevant and the likelihood rules the roost. We weren’t in that situation in 1995 - and we’re arguably still not - so we should still be guided, to some extent by what the prior tells us.

The form we found suggests that we can indeed reasonably assign most of our prior probability to the three special cases I have described. Since we also know that the Universe is neither totally empty nor ready to collapse, it does indicate that, in the absence of compelling evidence to the contrary, it is quite reasonable to have a prior preference for the case Ω=1. Until the late 1980s there was indeed a strong ideological preference for models with Ω=1 exactly, but not because of the rather simple argument given above but because of the idea of cosmic inflation.

From recent observations we now know, or think we know, that Ω is roughly 0.26. To put it another way, this means that the Universe has roughly 26% of the density it would need to have to halt the cosmic expansion at some point in the future. Curiously, this corresponds precisely to the unlikely or “fine-tuned” case where our Universe is in between two states in which we might have expected it to lie.

Even if you accept my argument that Ω=1 is a special case that is in principle possible, it is still the case that it requires the Universe to have been set up with very precisely defined initial conditions. Cosmology can always appeal to special initial conditions to get itself out of trouble because we don’t know how to describe the beginning properly, but it is much more satisfactory if properties of our Universe are explained by understanding the physical processes involved rather than by simply saying that “things are the way they are because they were the way they were.” The latter statement remains true, but it does not enhance our understanding significantly. It’s better to look for a more fundamental explanation because, even if the search is ultimately fruitless, we might turn over a few interesting stones along the way.

The reasoning behind cosmic inflation admits the possibility that, for a very short period in its very early stages, the Universe went through a phase where it was dominated by a third form of energy, vacuum energy. This forces the cosmic expansion to accelerate. This drastically changes the arguments I gave above. Without inflation the case with Ω=1 is unstable: a slight perturbation to the Universe sends it diverging towards a Big Crunch or a Big Freeze. While inflationary dynamics dominate, however, this case has a very different behaviour. Not only stable, it becomes an attractor to which all possible universes converge. Whatever the pre-inflationary initial conditions, the Universe will emerge from inflation with Ω very close to unity. Inflation trains our Universe to walk the tightrope.

So how can we reconcile inflation with current observations that suggest a low matter density? The key to this question is that what inflation really does is expand the Universe by such a large factor that the curvature radius becomes infinitesimally small. If there is only “ordinary” matter in the Universe then this requires that the universe have the critical density. However, in Einstein’s theory the curvature is zero only if the total energy is zero. If there are other contributions to the global energy budget besides that associated with familiar material then one can have a low value of the matter density as well as zero curvature. The missing link is dark energy, and the independent evidence we now have for it provides a neat resolution of this problem.

Or does it? Although spatial curvature doesn’t really care about what form of energy causes it, it is surprising to some extent that the dark matter and dark energy densities are similar. To many minds this unexplained coincidence is a blemish on the face of an otherwise rather attractive structure.

It can be argued that there are initial conditions for non-inflationary models that lead to a Universe like ours. This is true. It is not logically necessary to have inflation in order for the Friedmann models to describe a Universe like the one we live in. On the other hand, it does seem to be a reasonable argument that the set of initial data that is consistent with observations is larger in models with inflation than in those without it. It is rational therefore to say that inflation is more probable to have happened than the alternative.

I am not totally convinced by this reasoning myself, because we still do not know how to put a reasonable measure on the space of possibilities existing prior to inflation. This would have to emerge from a theory of quantum gravity which we don’t have. Nevertheless, inflation is a truly beautiful idea that provides a framework for understanding the early Universe that is both elegant and compelling. So much so, in fact, that I almost believe it."

And:

"A New Theory of the Universe

Yesterday I went on the train to London to visit my old friends in Mile End. I worked at the place that is now called Queen Mary, University of London for nearly a decade and missed it quite a lot when I moved to Nottingham. More recently I’ve had a bit more time and plausible excuses to visit London, including yesterday’s invitation to give a seminar at the Astronomy Unit. Although we were a bit late starting, owing to extremely slow service in the restaurant where we had lunch before the talk, it all seemed to go quite well. Afterwards we had a few beers and a nice chat before I took the train back to Cardiff again.

In the pub (which was the Half Moon, formerly the Half Moon Theatre, a place of great historical interest) I remembered a joke I sometimes make during cosmology talks but had forgotten to do in the one I had just given. I’m not sure it will work in written form, but here goes anyway.

I’ve blogged before about the current state of cosmology, but it’s probably a good idea to give a quick reminder before going any further. We have a standard cosmological model, known as the concordance cosmology, which accounts for most relevant observations in a pretty convincing way and is based on the idea that the Universe began with a Big Bang. However, there are a few things about this model that are curious, to say the least.

First, there is the spatial geometry of the Universe. According to Einstein’s general theory of relativity, universes come in three basic shapes: closed, open and flat. These are illustrated to the right. The flat space has “normal” geometry in which the interior angles of a triangle add up to 180 degrees. In a closed space the sum of the angles is greater than 180 degrees, and in an open space it is less. Of course the space we live in is three-dimensional but the pictures show two-dimensional surfaces.

But you get the idea.

The point is that the flat space is very special. The two curved spaces are much more general because they can be described by a parameter called their curvature which could in principle take any value (either positive for a closed space, or negative for an open space). In other words the sphere at the top could have any radius from very small (large curvature) to very large (small curvature). Likewise with the “saddle” representing an open space. The flat space must have exactly zero curvature. There are many ways to be curved, but only one way to be flat.

Yet, as near as dammit, our Universe appears to be flat. So why, with all the other options theoretically available to it, did the Universe decide to choose the most special one, which also happens in my opinion to be also the most boring?

Then there is the way the Universe is put together. In order to be flat there must be an exact balance between the energy contained in the expansion of the Universe (positive kinetic energy) and the energy involved in the gravitational interactions between everything in it (negative potential energy). In general relativity, you see, the curvature relates to the total amount of energy.

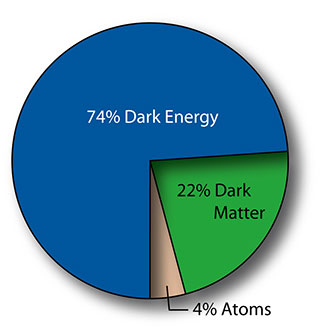On the left you can see the breakdown of the various components involved in the standard model with the whole pie representing a flat Universe. You see there’s a vary strange mixture dominated by dark energy (which we don’t understand) and dark mattter (which we don’t understand). The bit we understand a little bit better (because we can sometimes see it directly) is only 4% of the whole thing. The proportions look very peculiar.

And then finally, there is the issue that I talked about in my seminar in London and have actually blogged about (here and there) previously, which is why the Universe appears to be a bit lop-sided and asymmetrical when we’d like it to be a bit more aesthetically pleasing.

All these curiosities are naturally accounted for in my New Theory of the Universe, which asserts that the Divine Creator actually bought the entire Cosmos in IKEA.

This hypothesis immediately explains why the Universe is flat. Absolutely everything in IKEA comes in flat packs. Curvature is not allowed.

But this is not the only success of my theory. When God got home he obviously opened the flat pack, found the instructions and read the dreaded words “EASY SELF-ASSEMBLY”. Even the omnipotent would struggle to follow the bizarre set of cartoons and diagrams that accompany even the simplest IKEA furniture. The result is therefore predictable: strange pieces that don’t seem to fit together, bits left over whose purpose is not at all clear, and an overall appearance that is not at all like one would have expected.

It’s clear where the lop-sidedness comes in too. Probably some of the parts were left out so the whole thing isn’t held together properly and is probably completely unstable. This sort of thing happens all the time with IKEA stuff. And why is it you can never find the right size Allen Key to sort it out?

So there you have it. My new Theory of the Universe. Some details need to be worked out, but it is as good an explanation of these issues as I have heard. I claim my Nobel Prize.

If anything will ever get me a trip to Sweden, this will."